画像 場合の数 組み合わせ 公式 331940-場合の数 組み合わせ 公式
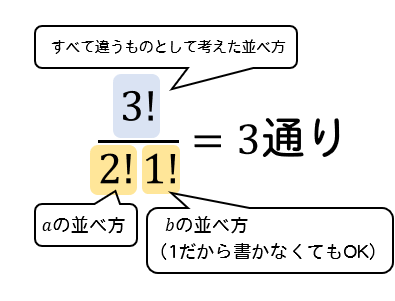
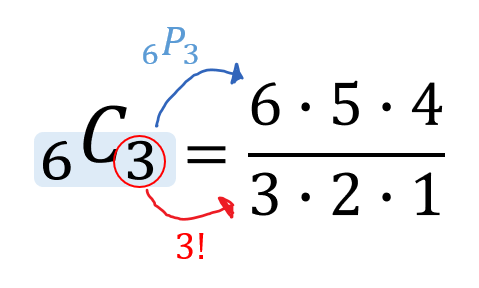
まだ公式(cとか!とかを使うもの)を習っていなかったのでこのサイトで調べました。 ドからシまでの12個の半音から7つの音を選んだ場合何通り作れるか 導入の検討をしている顔認識ツールに対する性能評価のため。 nC2としたとき十分な組み合わせの数順列の公式 は、 樹形図を 公式丸暗記では今後対応しきれません。 上記の仕組みをきっちり理解してください! 全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算をすればよいのか自明になります。 組み合わせ公式の確認 これは、この組み合わせの数の公式を使う事で 5C2=5×4÷2=10通り と求めることができます。 下のように表にして考えると「並びだけが違う、組み合わせとして見たら同じものが1セットにつき 2! =2 個ずつ存在する」のが分かりやすくなります。 「1
1
場合の数 組み合わせ 公式
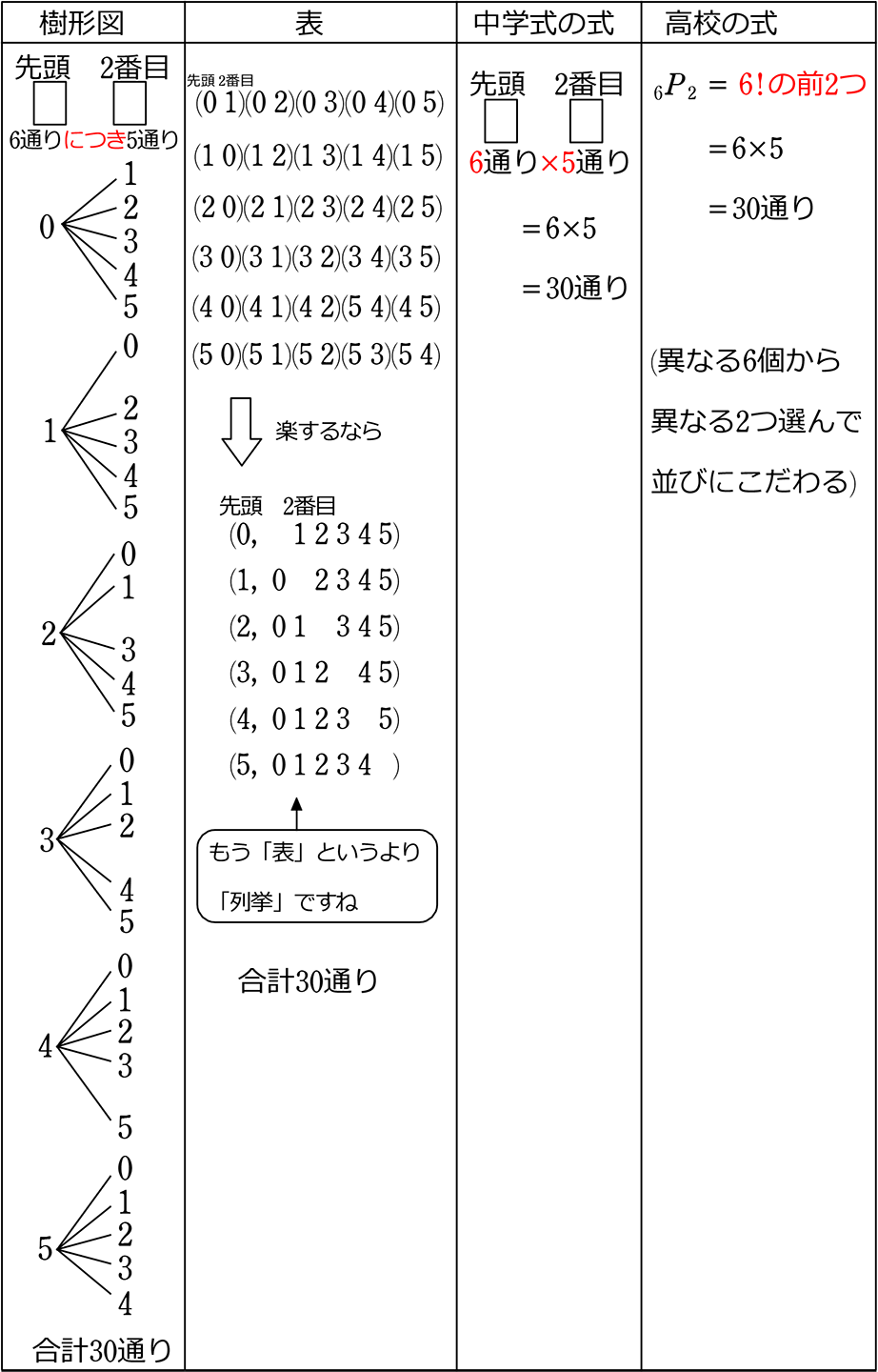
場合の数 組み合わせ 公式- ここまでの公式をまとめておきます。 どうやって作られたかも必ずみてくださいね。 Focus n 個から r 個を取り出して並べ換える場合の数は n P r = n × ( n − 1) × ⋯ ( n − r) n 個全てを並べ換える場合の数は n P n = n!順列の公式 は、 樹形図を 公式丸暗記では今後対応しきれません。 上記の仕組みをきっちり理解してください! 全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算をすればよいのか自明になります。




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
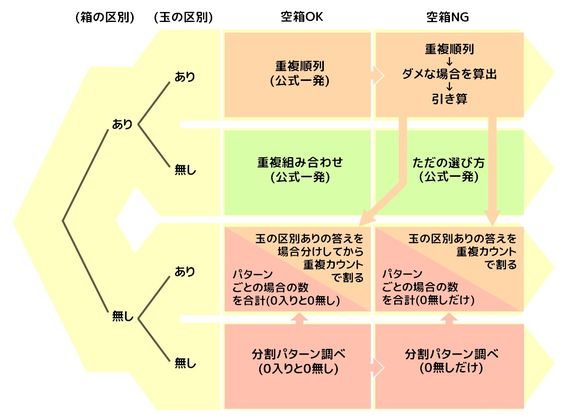
目標習得時間:2時間、問題数:7問 数学が好きか嫌いかの分かれ道 場合の数は、 「並べ方」「組み合わせ」「同じものを含む」「区別する」といった曖昧な概念が登場することから、数学が嫌いになる落とし穴の一つです。 しかし、これらの曖昧な概念はいくつかの解法パターンに分 例題(11)6人を部屋a、b、cに分ける場合の数を求めよ。但し空室があっても良いものとする。 場合の数と確率の分野では、原則として「人」は何も書いていない場合は区別します。 一人一人が3つの部屋の内から行きたい部屋を選ぶと考えて、3 6 =729(通り)// 順列のポイントは、 取り出す順番が関係する ということです。 つまり、「1回目にx、2回目にy、3回目にz を取り出したとき」を(x,y,z)で表すとすると、 (a,b,c)と(c,b,a)は 中身は同じですが、順番が違うため、別のものとしてカウントします。 一方で、 「組合せ(C)」では、順番を考慮しないの
(木) / (土) 組み合わせで出てくる の公式がたくさんありすぎて混乱してしまう。 このような悩みを解決します。 本記事では、組み合わせで登場する二項係数 についての重要公式9つを紹介し、その覚え方を解説します。 ※スマホの場合は グループ分けで明確にしておきたい2つのこと これまでに 順列 と 組合せ について学習しました。 順列 は選ぶだけでなく 並べ方 まで考慮した場合の数で、 組合せ は 選び方だけ を考慮した場合の数でした。 単純な順列や組合せであれば間違うことはないかもしれませんが、 グループ分け一連の記事はこちら 場合の数1|和の法則と積の法則は超アタリマエ! 場合の数2|順列のnPrの考え方と公式は超カンタン! 場合の数3|実はカンタンな円順列と数珠順列の考え方 場合の数4|組み合わせのnCrの求め方から性質まで攻略←今の記事
このことから場合の数と確率は非常に似ていることがわかります. そのため 確率を極めたければ,場合の数を極めるべし! では場合の数について見ていきましょう. 場合の数はどうやって求めるの? 条件に合うものを 書きだすのも1つの手 です= n × ( n − 1) × ⋯ × 2 × 1 で計算できる。場合の数・順列組み合わせの公式 場合の数の和の法則 A、Bという2つ同時には起こらない事象がある。Aの起こり方がm通り、Bの起こり方がn通りあるとき、AまたはBの起こる場合の数は、m+n通り 場合の数の積の法則 A、Bという2つの事



3




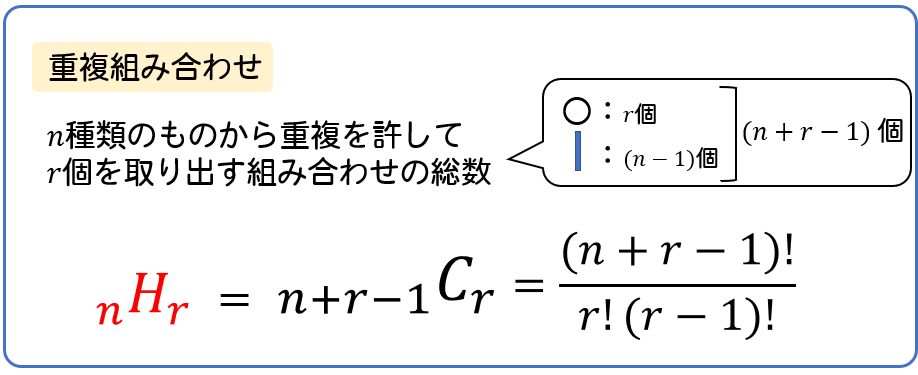
重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ
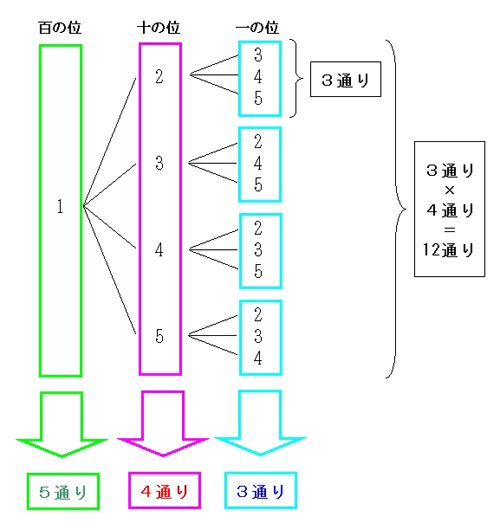
重複組み合わせの公式がどのようにして得られるのかを紹介しておきます。 「\(n\) 種類のものから重複を許して \(r\) 個選ぶ方法」は、「\(r\) 個のモノと \((n − 1)\) 個の仕切りを一列に並べる方法」と同じ場合の数になります。ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。 (1) 5 5 5 人の中から 2 2 2 人代表を選ぶ方法の数を求めよ。 (2) 5 5 5 人の中からリーダーと副リーダーを選ぶ方法の数を求めよ。 (3) 3 3 3 桁の正の整数で各桁の数字が 0 0 0 でなくて全て異なるものはいくつあるか。 (4) 47 47 47 都道府県から 5 5 5 つ選ぶ場合の数は




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
= 6 C 4 通り。 公式の証明は,上の例を一般化するだけです。 こんにちは、ももやまです。 今回は、 中学入試 高校入試 共通テスト(大学入試) spi(就職試験) 基本情報 など、様々な場面で出てくる場合の数、特に「順列と組み合わせの違い」に注目して説明していき そこで今回は、順列と組み合わせの違いを解説し、場合の数の単元において多くの方を悩ませる、 「積の法則」と「和の法則」の考え方の違い をご紹介します。 コンテンツ 非表示 1 順列と組み合わせの違いは? 2 積の法則=各事象が同時に起こりうる




高校数学 数a 4 場合の数 基本編 Youtube




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
= 6 C 4 \dfrac{6!}{4!2!}={}_6\mathrm{C}_4 4!場合の数5|同じものを含むと順列の場合の数はどう変わる? 場合の数6|重複組み合わせは2パターンでok! 場合の数7|二項定理を理解しよう!場合の数を使って導出! 場合の数8|展開が楽にできる「パスカルの三角形」の考え方になります。n 個の要素から 3 つを取り出す場合の組み合わせであれば、重複数は必ず \({}_3P_3=3!\) になります。つまり公式から組み合わせを求める際の分母は \({}_rP_r=r!\) で求められるのです。



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




高校 数学a 場合の数24 組合せの計算 15分 Youtube




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



1



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




高校数学a 組合せの活用4 少なくとも 練習編 映像授業のtry It トライイット




4年生向け 中学受験 算数 場合の数 組み合わせ計算 5人から 人を選びます コンビネーションを使った計算方法を例題とともに解説します Youtube




確率の問題の解き方 場合の数 組み合わせ と確率 現役塾講師のわかりやすい中学数学の解き方
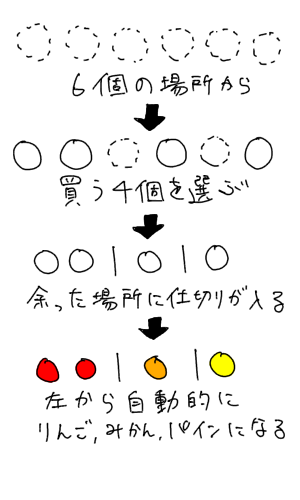



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書
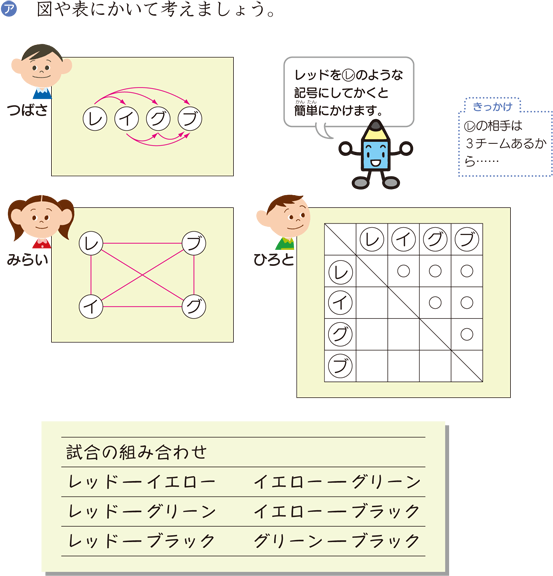



場合の数 算数用語集
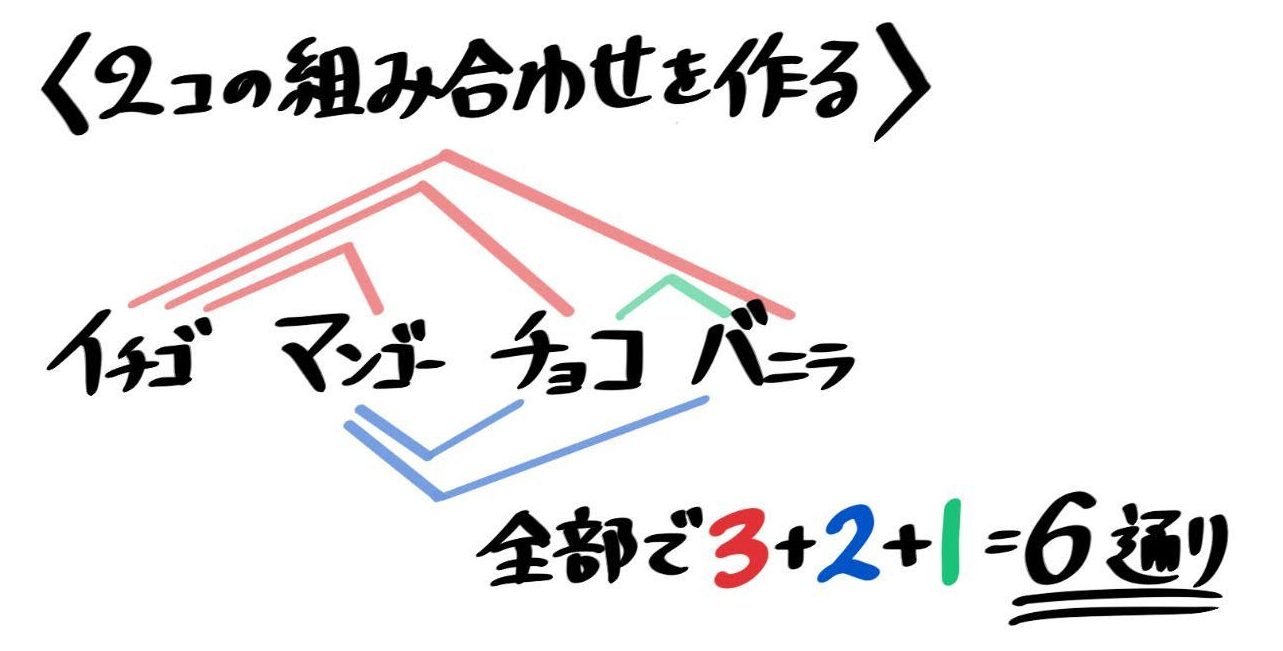



中学受験 場合の数の問題 解き方の総まとめ 数字カード 道順 色分け等 そうちゃ式 受験算数 新1号館 数論 特殊算



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ
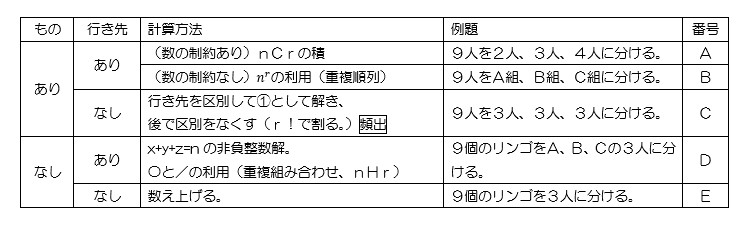



場合の数 確率を体系的に学ぼう 教科書でバラバラに登場するパターンを整理して把握しよう オンライン受講 東大に 完全 特化 東大合格 敬天塾




数学a 場合の数 組分け Youtube




4年生向け 中学受験 算数 場合の数 組み合わせ計算 黒のボール2個と白のボール4個の並べ方をコンビネーションを使って求める方法を例題とともに解説します Youtube




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート



2
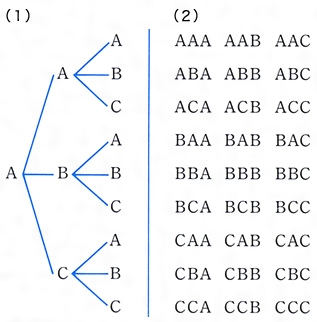



場合の数とは コトバンク




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
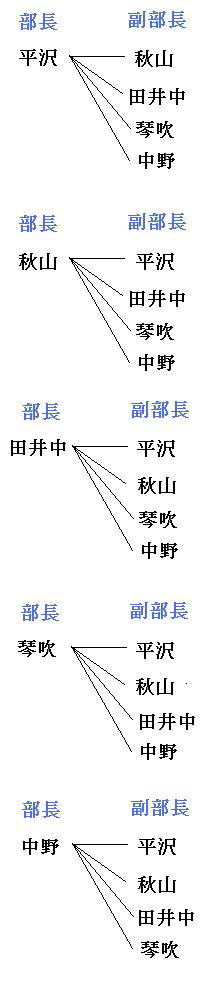



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける
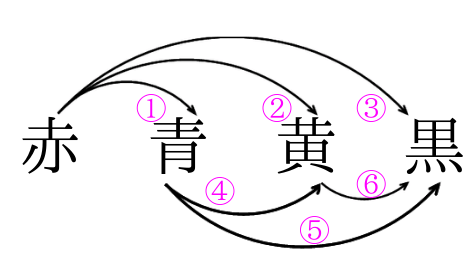



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校
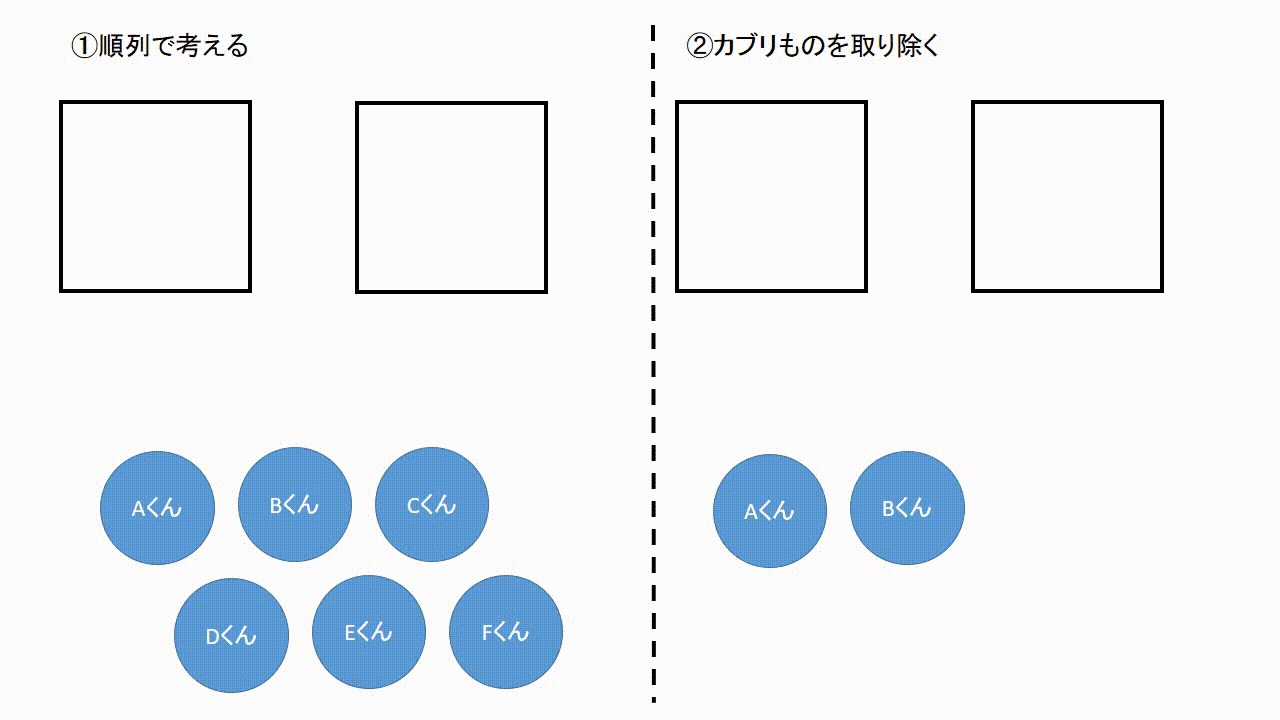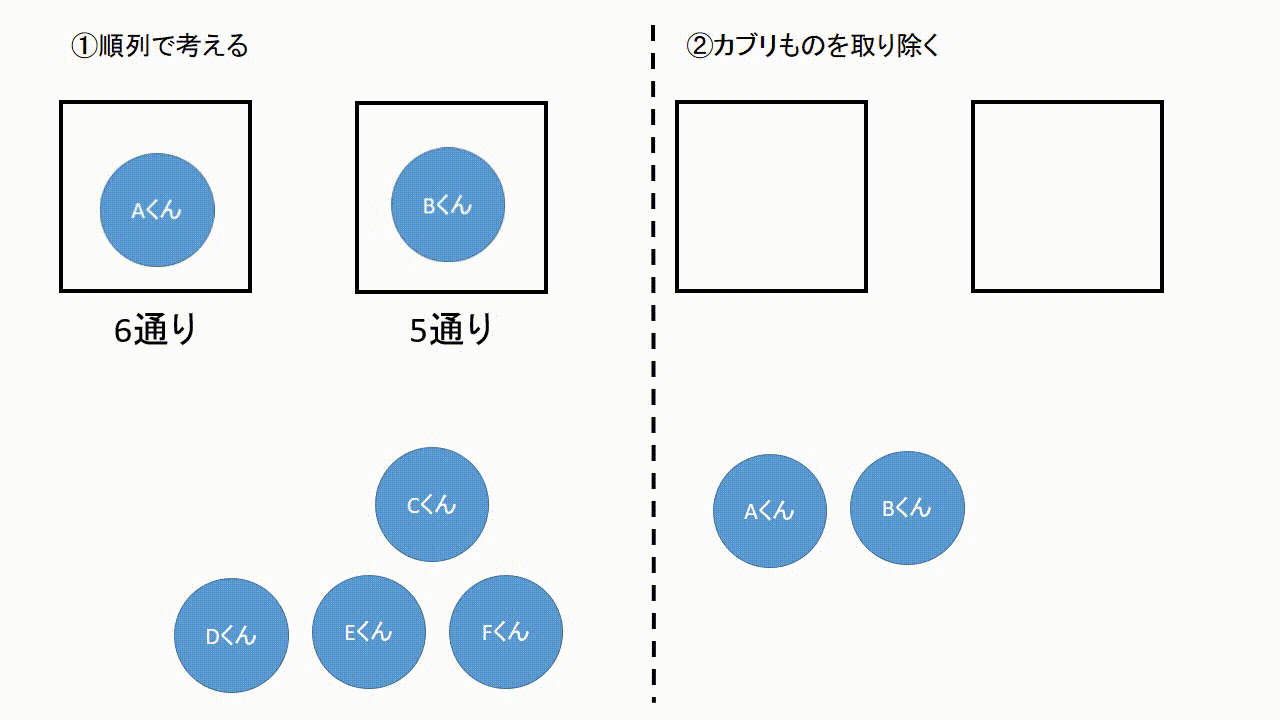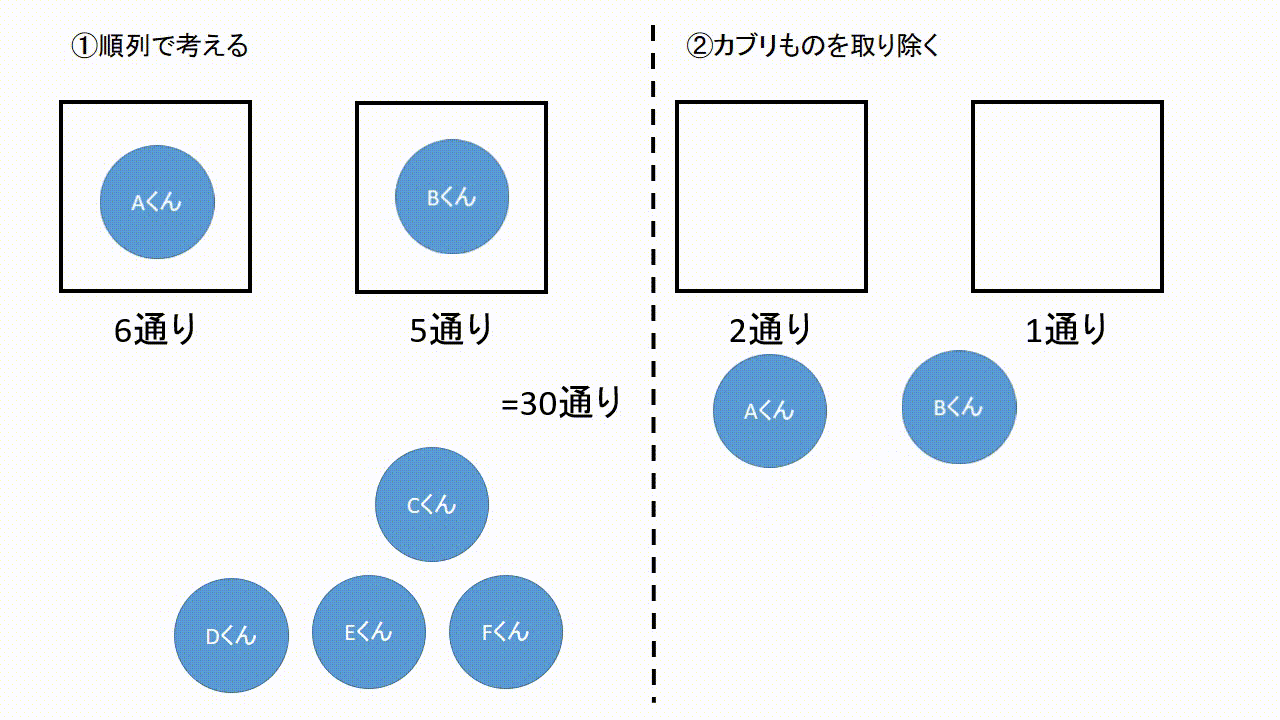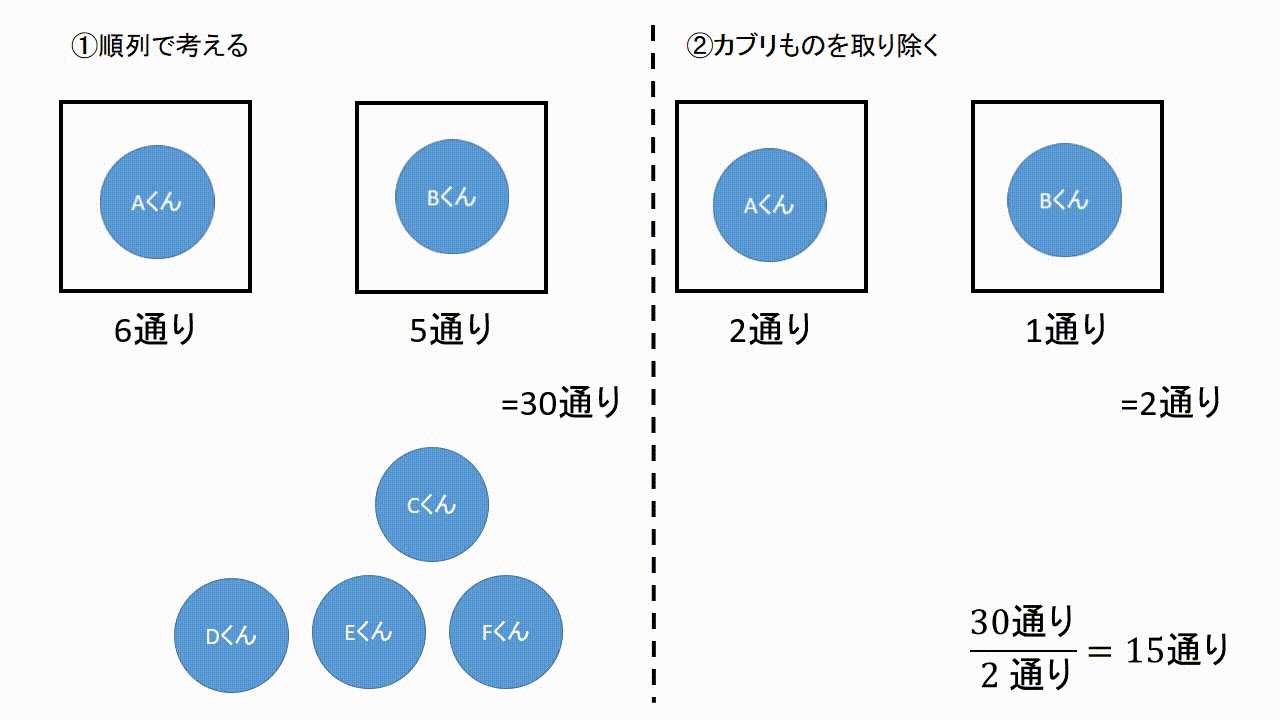



数学 確率を極めるには 場合の数 を極めろ




組み合わせncrはどう計算する 求め方から性質までを攻略



重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ



場合の数



中学数学 場合の数




5分で分かる 確率統計 Ncr の計算方法 あぱーブログ




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説



計算するから難しい 小学生の場合の数は 数え方 が大事 みけねこ小学校




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clearnote




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
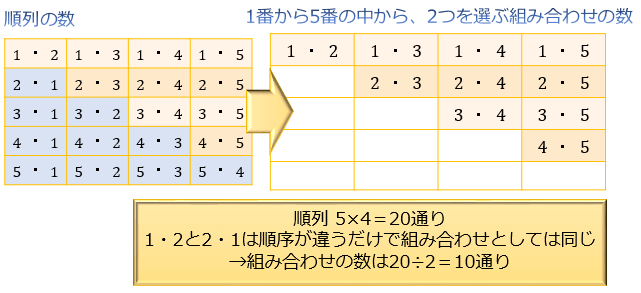



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



場合の数 Of 京極一樹の数学塾会員頁




場合の数と確率
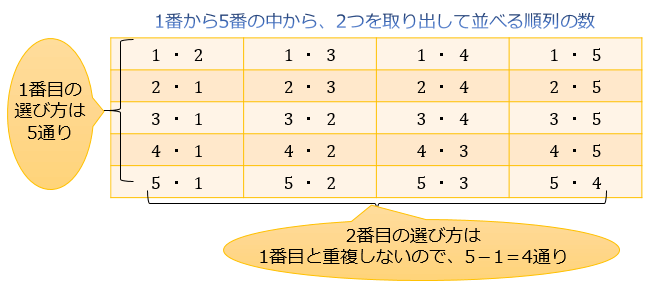



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



重複組合せ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



1




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




数学a 場合の数 組み合わせの総数 Youtube




中学数学 場合の数




場合の数 順列組み合わせの公式一覧 数学a By となりがトトロ マナペディア



場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




順列pと組み合わせcの違いと 簡単 な見分け方
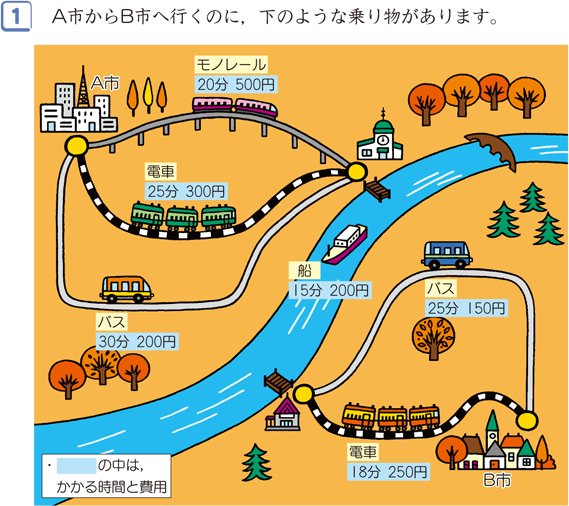



場合の数 算数用語集




数学 Ncr 組み合わせ コンビネーションの計算方法と意味




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




四谷大塚 場合の数 に苦手意識を持っているようです 中学受験 個別指導のss 1



順列と組み合わせの違いと見分け方 公式や練習問題 受験辞典




順列と組み合わせの公式とその違い 問題付き 理系ラボ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



場合の数 学び家 Com




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




高校数学 数a 14 組み合わせ 基本編 Youtube




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




この問題で場合の数を計算する時に なぜさいころの目が出る順番まで考慮しなきゃ Clearnote




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ



場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




順列と組み合わせの公式とその違い 問題付き 理系ラボ



Lh3 Googleusercontent Com Proxy Tqxhcgljzmpac9lfshbe4mngzpd6u Wkczx Uf1xqawmjk3nmjxreqj5m Sahxwnrvvf1o Mf3mx0f34i 7lxl2cpph 1fcdxhekynidmpfgtgrbsfkjp158 W38cwdjujojk4uye16nff Hjpdb5uzfrwzrxyzt0fjqe9u5




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ



中学数学 場合の数



1




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



組み分け 部屋分け 問題全8パターンと解き方 数a 場合の数確率 そうちゃ S 図解英数ゼミナール




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




順列の問題 一定の条件で並べる 高校数学の知識庫




6年算数 並べ方と組み合わせ方 場合の数 の教え方



重複組合せの考え方 思考力を鍛える数学
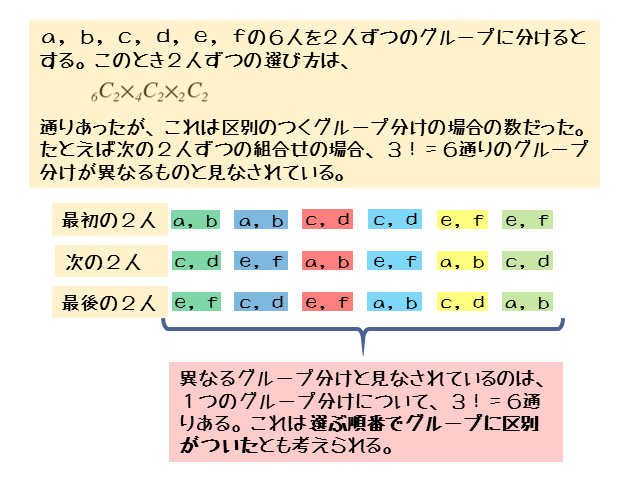



場合の数 グループ分けについて 日々是鍛錬 ひびこれたんれん



9 3 確率の計算 順列 組み合わせ 統計学の時間 統計web




リンゴ9個 重複組合せ 解説その1 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




組み合わせの総数 場合の数 理数系無料オンライン学習 Kori




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方




場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典

No comments: